 Created from Youtube video: https://www.youtube.com/watch?v=4srS0s1d9Ywvideo
Created from Youtube video: https://www.youtube.com/watch?v=4srS0s1d9YwvideoConcepts covered:rotation matrices, reference frames, orthogonality, invariance, Euclidean norm
The video explains the concept of rotation matrices, which are fundamental in describing the relative orientation between reference frames. It covers the construction of rotation matrices, their properties such as orthogonality, invariance under rotation, and how multiplying rotation matrices results in another rotation matrix.
Table of Contents1.Understanding Rotation Matrices and Reference Frames2.Properties of Rotation Matrices3.Properties and Implications of Rotation Matrices
chapter
1
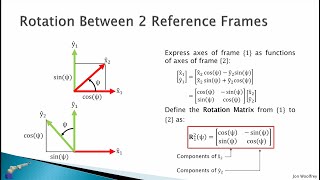
Understanding Rotation Matrices and Reference Frames
Concepts covered:rotation matrices, reference frames, trigonometry, orientation, 2D rotations
This chapter introduces rotation matrices, which are essential for describing the relative orientation between different reference frames. It explains how to mathematically express the orientation of one frame with respect to another using trigonometry and matrix operations, focusing on 2D rotations.
Question 1
Rotation matrices describe orientation between reference frames.
Question 2
What is the purpose of rotation matrices?
Question 3
We describe the relative orientation between _____ frames using rotation matrices.
Question 4
CASE STUDY: A drone needs to align its camera with a moving object. The drone's base orientation is known, and the camera's orientation relative to the base is given. The object's orientation relative to the camera is also provided.
All of the following are correct applications of rotation matrices except...
Question 5
CASE STUDY: In a virtual reality system, the orientation of the user's headset relative to the room and the orientation of the virtual objects relative to the headset are known.
Select three correct applications of rotation matrices.
chapter
2
Properties of Rotation Matrices
Concepts covered:rotation matrix, inverse, Euclidean norm, determinant, orthogonal
The chapter explains that the inverse of a rotation matrix is its transpose, and the Euclidean norm and determinant of a rotation matrix are both 1. It also discusses the orthogonality of rotation matrices and how their properties ensure that the area or volume bounded by the axes remains constant during rotation.
Question 6
Is the inverse of a rotation matrix its transpose?
Question 7
Why is a rotation matrix orthogonal?
Question 8
The rotation matrix is orthogonal because its column vectors are _____.
Question 9
CASE STUDY: A robot arm is rotating from position A to position B. The rotation is described by the matrix R_A_to_B. You need to find the rotation matrix from position B back to position A.
All of the following are correct applications of rotation matrix properties except...
Question 10
CASE STUDY: You are implementing a feature in a CAD software that requires rotating objects without altering their shape or size. You use rotation matrices for this purpose.
Select three correct properties of rotation matrices.
chapter
3
Properties and Implications of Rotation Matrices
Concepts covered:rotation matrix, invariance, special orthogonal group, Euclidean norm, vector magnitude
This chapter discusses the properties and implications of rotation matrices, particularly their invariance under rotation. It explains how the magnitude of a vector remains unchanged when rotated and how multiplying rotation matrices results in another rotation matrix, emphasizing their role in describing relative orientations between reference frames.
Question 11
Multiplying two rotation matrices results in another rotation matrix.
Question 12
What results from multiplying two rotation matrices?
Question 13
Rotation matrices describe relative orientation between _____ frames.
Question 14
CASE STUDY: A physics student is studying the motion of a particle in a rotating reference frame. They use rotation matrices to transform the particle's velocity vector between reference frames.
All of the following are true about rotation matrices except...
Question 15
CASE STUDY: An animator is creating a 3D animation of a rotating cube. They use rotation matrices to animate the cube's rotation.
Select three correct characteristics of rotation matrices.
Would you like to create and run this quiz?
yesCreated with Kwizie
