Relations and Functions | Algebra

Created from Youtube video: https://www.youtube.com/watch?v=wbBY2tTqXDAvideo

Concepts covered:relations, functions, domain, range, vertical line test

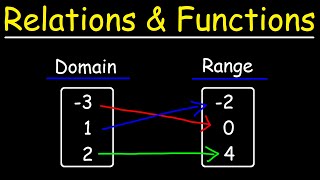
The video explains the concepts of relations and functions in algebra, focusing on how to identify the domain and range of a relation and determine if a relation is a function. It introduces methods such as mapping diagrams, function tables, and the vertical line test to assess whether a relation qualifies as a function, emphasizing that a function must have each input value corresponding to exactly one output value.

Table of Contents1.Understanding Relations and Functions 2.Determining Functions Using Mapping Diagrams 3.Determining Functions Using Tables and Graphs

chapter

Understanding Relations and Functions

Concepts covered:relations, functions, domain, range, input-output pairs

The chapter explains the concept of relations and functions, focusing on how to identify the domain and range of a relation and determine if a relation is a function. A relation is a set of input-output pairs, and it is a function if each input has a unique output; repeating input values with different outputs indicate it is not a function.

Question 1

A function has unique output for each input value.

Question 2

How do you list the domain of a relation?

Question 3

If an input has multiple outputs, the relation is not a _____.

Question 4

CASE STUDY: A teacher is creating a grading system where each student ID is paired with a grade. The teacher wants to ensure the system is a function.

What ensures the grading system is a function?

Question 5

CASE STUDY: A researcher is analyzing a set of experimental results, where each experiment number is paired with a result value. The researcher needs to confirm the data's functional integrity.

Select three criteria for functional integrity.

Question 6

The range of a relation includes all input values.

Question 7

What indicates a relation is not a function?

Question 8

A relation is a set of pairs of _____ and output values.

Question 9

CASE STUDY: A data analyst is reviewing a dataset of customer transactions. Each transaction is represented as an ordered pair of customer ID and transaction amount. The analyst needs to determine if the dataset can be considered a function.

Which condition disqualifies the dataset as a function?

Question 10

The domain of a relation consists of all x-values.

Question 11

What is the range in a relation?

Question 12

A function requires each input to have only one _____ value.

Question 13

A relation is not a function if x-values repeat with different y-values.

Question 14

What defines a relation in mathematics?

Question 15

A relation with repeating x-values is always a function.

Question 16

How is a function different from a relation?

chapter

Determining Functions Using Mapping Diagrams

Concepts covered:mapping diagram, relation, function, domain, range

The chapter explains how to create mapping diagrams for relations to determine if they are functions. The first relation is a function as each domain value maps to a unique range value, while the second relation is not a function due to repeated domain values mapping to different range values.

Question 17

Is a relation with unique x-values a function?

Question 18

What defines a relation as a function?

Question 19

In a mapping diagram, the domain consists of _____ values.

Question 20

CASE STUDY: A website offers resources for learning about functions and relations.

Identify the incorrect website feature.

Question 21

Can a function have multiple outputs for one input?

Question 22

What is the range in a mapping diagram?

Question 23

To receive updates, join the _____ list on the website.

Question 24

CASE STUDY: A teacher is explaining functions using mapping diagrams to students.

Identify the incorrect function mapping.

Question 25

Repeated x-values indicate a relation is not a function.

Question 26

What is the domain in a mapping diagram?

Question 27

A repeat x-value with different y-values indicates _____ a function.

Question 28

Mapping diagrams help visualize relations and functions.

Question 29

How can you identify a non-function relation?

Question 30

A relation is a function if each input has _____ output.

chapter

Determining Functions Using Tables and Graphs

Concepts covered:function table, vertical line test, relation, input values, output values

The chapter explains how to determine if a relation is a function by using a function table and the vertical line test. It highlights that a relation is not a function if an input corresponds to multiple outputs or if a vertical line intersects a graph at more than one point.

Question 31

Does a circle pass the vertical line test?

Question 32

What indicates a relation is not a function?

Question 33

In a function table, the domain corresponds to the _____ values.

Question 34

CASE STUDY: A data analyst is reviewing a graph to determine if it represents a function. They use the vertical line test and find that a vertical line intersects the graph at multiple points.

Identify the incorrect application of the vertical line test.

Question 35

CASE STUDY: An engineer is designing a system and needs to ensure that each input has a unique output. They are reviewing a function table to verify this.

Select three correct applications of function table analysis.

Question 36

Is a relation with multiple vertical line intersections a function?

Question 37

What is the domain in a function table?

Question 38

A graph represents a function if a vertical line touches it at _____ point.

Question 39

CASE STUDY: A teacher is explaining how to determine if a relation is a function using a function table. The students are given a table with input values and corresponding output values. They notice that one input value has two different output values.

Identify the incorrect application of function table analysis.

Question 40

Can a function have identical x-values with different y-values?

Question 41

What determines if a relation is a function?

Question 42

The input values in a function table represent the _____ values.

Question 43

Does the vertical line test determine if a graph is a function?

Question 44

How to list repeat values in a function table?

Question 45

A relation is not a function if it fails the _____ line test.

Question 46

Is a relation with unique x-values a function?

Question 47

How do you identify a function from a graph?

Question 48

If two identical x values have different y values, the relation is _____ a function.

Create your own quiz for this video

Would you like to create and run this quiz?

yesno

Created with Kwizie